Analyse du profil des étudiants d’un MOOC
Cette analyse a été réalisée en collaboration avec Avner.
Cette page présente une analyse statistique effectuée sur le profil des étudiants du MOOC « Fondamentaux en Statistique » qui a été publié sur la plate-forme France Université Numérique (FUN) le 16 janvier 2014 pour une durée de 5 semaines. Un questionnaire auto-déclaratif conçu par FUN et proposé aux étudiants lors de leur inscription a permis d’obtenir des informations sur les étudiants. Nous présentons ici une analyse simple de leur profil. Cette analyse est réalisée avec le logiciel statistique libre R et les packages :
library(OpenStreetMap)
library(ggplot2)
library(xtable)
library(FactoMineR)
L’analyse requiert l’importation dans l’espace de travail de R des fichiers anonymousStudents-FUN.csv (fichier contenant les informations sur les étudiants obtenues à partir du questionnaire auto-déclaratif) et addresses-FUN.csv (fichier contenant les informations sur les étudiants obtenues à partir des déclarations et des API de géo-localisation de Google Map et de Open Street Map). Les fichiers sont importés à partir des commandes :
students = read.csv("anonymousStudents-FUN.csv", stringsAsFactor=FALSE,
fileEncoding="UTF8")
addresses = read.csv("addresses-FUN.csv", fileEncoding="UTF8")
Le nombre de répondants au questionnaire est 6918.
Analyse du sexe
Dans cette partie, nous étudions tout d’abord le sexe des étudiants dont la répartition est donnée dans le tableau ci-dessous :
students$gender[students$gender%in%c("","None")] = NA
outGender = as.matrix(table(students$gender))
rownames(outGender) = c("Femmes", "Hommes")
colnames(outGender) = "Effectifs"
print(xtable(outGender), type="html")
| Effectifs | |
|---|---|
| Femmes | 2108 |
| Hommes | 4493 |
outGender = outGender/sum(!is.na(students$gender))*100
colnames(outGender) = "Fréquences (%)"
print(xtable(outGender, digits=1), type="html")
| Fréquences (%) | |
|---|---|
| Femmes | 31.9 |
| Hommes | 68.1 |
Ceci nous montre que moins de $\frac{1}{3}$ des étudiants sont des étudiantes.
Analyse de l’âge
Cette partie s’intéresse à l’âge des étudiants :
students$age = 2013 - as.numeric(students$year_of_birth)
Le nombre d’étudiants ayant déclaré avoir moins de 13 ans est 38 et le nombre d’étudiants ayant déclaré avoir plus de 100 ans est 2. Ces étudiants sont supprimés de l’analyse :
students$age[students$age<=13|students$age>100] = NA
ageSummary = as.matrix(summary(students$age))
colnames(ageSummary) = "valeur"
rownames(ageSummary) = c("minimum", "Q1", "médiane", "moyenne", "Q3",
"maximum", "valeur manquante")
print(xtable(ageSummary, digits=2), type="html")
| valeur | |
|---|---|
| minimum | 14.00 |
| Q1 | 26.00 |
| médiane | 34.00 |
| moyenne | 35.57 |
| Q3 | 43.00 |
| maximum | 84.00 |
| valeur manquante | 439.00 |
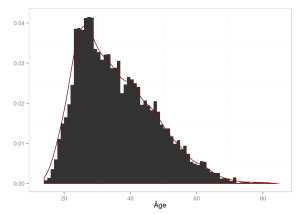
Le nombre d’étudiants pour lequel l’âge est connu est donc 6479, ce qui correspond à 93.65% des étudiants ayant rempli le questionnaire. La figure ci-dessous montre la répartition de l’âge des étudiants :
p = ggplot(students, aes(x=age)) +
geom_histogram(aes(y=..density..), binwidth=1) +
geom_density(linewidth=2, colour="darkred") + xlab("Âge") + ylab("") +
theme(panel.background=element_rect(fill="white", colour="grey"))
print(p)
Celle-ci permet de constater que beaucoup d’étudiants ont entre 25 et 35 ans, avec des étudiants beaucoup plus âgés (l’âge maximum étant 84 ans).
Analyse du niveau d’études
La répartition des divers niveaux d’études parmi la population des étudiants est donnée dans le tableau ci-dessous :
students$level_of_education[students$level_of_education=="a"] =
"Licence professionnelle"
students$level_of_education[students$level_of_education=="b"] = "Licence"
students$level_of_education[students$level_of_education=="el"] = "Brevet"
students$level_of_education[students$level_of_education=="hs"] = "Baccalauréat"
students$level_of_education[students$level_of_education=="jhs"] = "DUT/BTS"
students$level_of_education[students$level_of_education=="m"] = "Master"
students$level_of_education[students$level_of_education=="none"] =
"Aucun"
students$level_of_education[students$level_of_education=="other"] = "Autre"
students$level_of_education[students$level_of_education=="p"] = "Doctorat"
students$level_of_education[students$level_of_education%in%c("","None")] = NA
students$level_of_education = factor(students$level_of_education,
levels=c("Aucun", "Brevet", "Baccalauréat", "DUT/BTS",
"Licence professionnelle", "Licence", "Master", "Doctorat",
"Autre"),
ordered=TRUE)
outEducation = as.matrix(table(students$level_of_education))
colnames(outEducation) = "Effectif"
print(xtable(outEducation), type="html")
| Effectif | |
|---|---|
| Aucun | 27 |
| Brevet | 65 |
| Baccalauréat | 497 |
| DUT/BTS | 546 |
| Licence professionnelle | 178 |
| Licence | 967 |
| Master | 3208 |
| Doctorat | 937 |
| Autre | 188 |
Le nombre d’étudiants pour lequel on connaît le niveau d’études est donc 6613 soit environ 95.59% des étudiants ayant rempli le questionnaire. Parmi ceux-ci, la fréquence d’étudiants de master est 48.51%. Les personnes suivant le cours le suivent donc probablement dans le cadre d’un enrichissement personnel de leur niveau de formation puisque le type d’enseignement dispensé dans le cours « Fondamentaux en Statistique » se situe généralement en premier cycle d’un cursus universitaire en France.
Relation entre âge et niveau d’études
Une analyse factorielle des correspondances (AFC) permet de préciser la relation entre âge et niveau d’études (voir « Saporta (1990) Probabilités, analyse des données et statistique. Editions Technip » pour une introduction à l’AFC) :
breakDates = c(1900,1961,1967,1972,1976,1980,1983,1986,1988,1991,2013)
students$age_class = cut(students$age, breaks=2013-breakDates,
labels=c("22 ans et moins", "23-25 ans",
"26-27 ans", "28-30 ans", "31-33 ans",
"34-37 ans", "38-41 ans", "42-46 ans",
"47-52 ans", "53 ans et plus"))
curDF = na.omit(data.frame(age=students$age_class,
education=students$level_of_education))
resCA = CA(table(curDF), graph=FALSE)
plot(resCA, axes=1:2, title="")
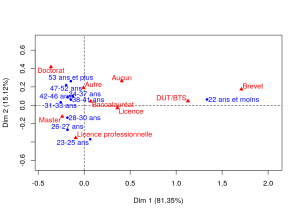
81.35% de la variance est expliquée par l’axe 1 et 15.12% par l’axe 2. Le premier plan factoriel représente donc 96.47% de la variance : de manière claire, celui-ci sépare les plus jeunes (moins de 22 ans, qui sont probablement encore dans le système scolaire) du reste des autres étudiants. Ils ont la particularité d’avoir un plus faible niveau d’études (qui s’explique au moins en partie par leur âge), Brevet et DUT/BTS en particulier. Le deuxième axe oppose les étudiants ayant suivi des études plutôt courtes et professionnalisantes (licence professionnelle) qui sont plutôt jeunes (moins de 30 ans) aux les étudiants ayant suivi des études plus longues (doctorat) et qui sont plus âgés (plus de 47 ans).
Analyse de la localisation géographique
Étudiants français
Dans un premier temps, nous analysons la localisation géographique des étudiants habitant en France :
coordFrance = addresses[which(addresses$country=="France"),]
Le nombre d’étudiants ayant déclaré être localisé en France est 2826. Les principales villes où sont localisés les étudiants sont listées ci-dessous :
frenchTable = table(coordFrance[,3])
outFrench = as.matrix(head(frenchTable[order(frenchTable,decreasing=TRUE)],
n=11))
colnames(outFrench) = "Effectif"
outFrench = xtable(outFrench, align="|l|c|")
print(outFrench, type="html")
| Effectif | |
|---|---|
| Paris | 388 |
| Lyon | 49 |
| Marseille | 46 |
| Toulouse | 41 |
| Montpellier | 33 |
| Strasbourg | 31 |
| Bordeaux | 26 |
| Nantes | 23 |
| Versailles | 21 |
| Nice | 20 |
| Rennes | 20 |
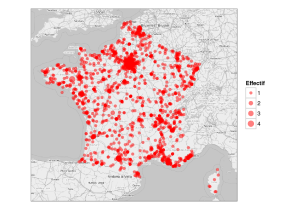
De manière plus précise, la localisation géogrpahique des étudiants français peut être visualisée sur une carte obtenue à partir des fonds de carte de Open Street Map (l’aire des disques est proportionnelle à l’effectif) :
franceData = data.frame(coordFrance,
students[which(addresses$country=="France"),])
onlyUniqueCoord = unique(coordFrance)
onlyUniqueCoord = onlyUniqueCoord[which(!is.na(onlyUniqueCoord[,1])),]
# remove strange point
onlyUniqueCoord = onlyUniqueCoord[-c(2596),]
mapDF = data.frame(projectMercator(onlyUniqueCoord[,1],
onlyUniqueCoord[,2]))
mapDF$size = sapply(1:nrow(onlyUniqueCoord), function(ind)
sum(coordFrance[,1]==onlyUniqueCoord[ind,1] &
coordFrance[,2]==onlyUniqueCoord[ind,2], na.rm=TRUE))
frenchMap = openmap(c(51.700,-5.669), c(41,11), type="osm-bw")
p = autoplot(frenchMap) +
geom_point(aes(x=x,y=y,size=size), colour=heat.colors(20,alpha=0.5)[1],
data=mapDF) +
theme_bw() + scale_size_area(max_size=5) + labs(size="Effectif") +
theme(axis.title.x=element_blank(), axis.ticks=element_blank(),
axis.text.x=element_blank(), axis.title.y=element_blank(),
axis.text.y=element_blank())
print(p)
Ensemble des étudiants
On analyse maintenant la localisation géographique des étudiants du monde entier.
worldData = data.frame(addresses[!is.na(addresses[,1]),],
students[!is.na(addresses[,1]),])
Le nombre d’étudiants dont on connait la localisation géographique est 3730 ce qui correspond à environ 53.92% des étudiants ayant répondu au questionnaire. Par ailleurs, le nombre d’étudiants localisés en Franche correspond à environ 75.76% des étudiants dont on connaît la localisation.
Les principaux pays dont sont issus les étudiants sont :
worldTable = table(worldData$country)
outWorld = as.matrix(head(worldTable[order(worldTable,decreasing=TRUE)], n=14))
colnames(outWorld) = "Effectif"
outWorld = xtable(outWorld, align="|l|c|")
print(outWorld, type="html")
| Effectif | |
|---|---|
| France | 2826 |
| Morocco | 94 |
| United States | 78 |
| Algeria | 60 |
| Belgium | 45 |
| Senegal | 39 |
| Canada | 38 |
| Cameroon | 36 |
| Tunisia | 33 |
| Switzerland | 29 |
| Côte d’Ivoire | 28 |
| Mali | 21 |
| Benin | 20 |
| Burkina Faso | 20 |
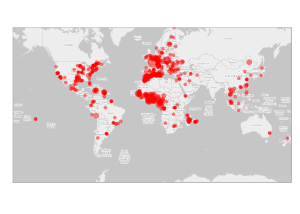
ce qui permet d’identifier qu’un grand nombre d’étudiants localisés à l’étranger sont issus de l’Afrique francophone. De manière plus complète, la localisation géographique des étudiants est donnée par la carte suivante (l’aire des disques est proportionnelle au $\log_2$ de l’effectif afin de ne pas sur-représenter la France métropolitaine qui est représentée par un seul point) :
indParis = which(worldData[,3]=="Paris")[1]
worldData[which(worldData[,4]=="France"),1:2] =
worldData[indParis,1:2]
onlyUniqueCoord = unique(worldData[,1:2])
mapDF = data.frame(projectMercator(onlyUniqueCoord[,1],
onlyUniqueCoord[,2]))
mapDF$size = sapply(1:nrow(onlyUniqueCoord), function(ind)
log2(sum(worldData[,1]==onlyUniqueCoord[ind,1] &
worldData[,2]==onlyUniqueCoord[ind,2]))+1)
worldMap = openmap(c(70,-179), c(-70,179), type="osm-bw")
p = autoplot(worldMap) +
geom_point(aes(x=x,y=y,size=size), colour=heat.colors(20,alpha=0.5)[1],
data=mapDF) + theme_bw() + scale_size_area(max_size=10) +
theme(axis.title.x=element_blank(), axis.ticks=element_blank(),
axis.text.x=element_blank(), axis.title.y=element_blank(),
axis.text.y=element_blank(), legend.position="none")
print(p)